Data structures are an essential part of computer science and programming, as they allow us to efficiently store and manipulate data. C#, a popular programming language, provides several built-in data structures that can be used to store and organize data in a variety of ways. In this article, we will explore some of the most common data structures in C# and provide examples of how they can be used in practice.
Arrays
Arrays are a simple data structure that allows us to store a fixed-size sequential collection of elements. Each element in an array is accessed by its index, which is a numerical position in the array. In C#, arrays can be declared as follows:
int[] arr = new int[5]; // Declare an array of integers with 5 elements
string[] strArr = new string[3]; // Declare an array of strings with 3 elements
We can also initialize an array with values at the time of declaration:
int[] arr = new int[] {1, 2, 3, 4, 5}; // Declare and initialize an array of integers
string[] strArr = new string[] {"apple", "banana", "cherry"}; // Declare and initialize an array of strings
To access and modify the elements of an array, we can use the index operator ([]):
int[] arr = new int[5];
arr[0] = 1; // Set the first element of the array to 1
arr[4] = 5; // Set the last element of the array to 5
int x = arr[2]; // Get the third element of the array and store it in x
Lists
Lists are a dynamic data structure that allows us to store a collection of elements that can grow or shrink as needed. In C#, lists are implemented using the List<T> class, where T is the type of elements that the list will store. Lists can be declared and initialized as follows:
List<int> list = new List<int>(); // Declare an empty list of integers
List<string> strList = new List<string>() {"apple", "banana", "cherry"}; // Declare and initialize a list of strings
We can use the Add method to add elements to a list:
List<int> list = new List<int>();
list.Add(1); // Add the integer 1 to the list
list.Add(2); // Add the integer 2 to the list
We can access and modify the elements of a list using the index operator ([]):
List<int> list = new List<int>() {1, 2, 3};
list[0] = 4; // Set the first element of the list to 4
int x = list[1]; // Get the second element of the list and store it in x
Stacks
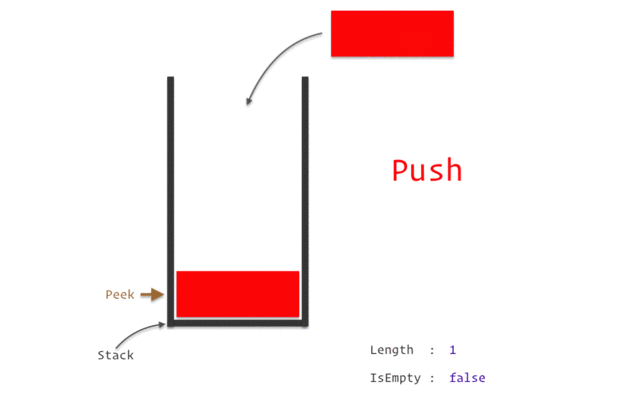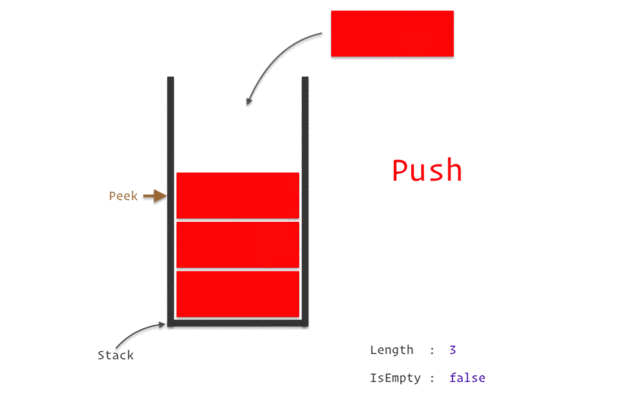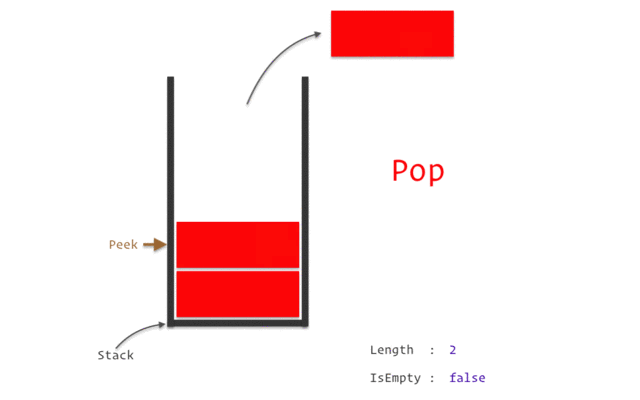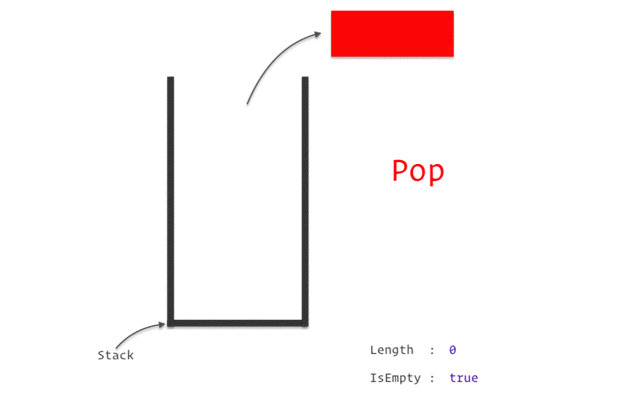
Stacks are a data structure that follows the Last In First Out (LIFO) principle, meaning that the last element added to the stack will be the first one to be removed. In C#, stacks are implemented using the Stack<T> class, where T is the type of elements that the stack will store. Stacks can be declared and initialized as follows:
Stack<int> stack = new Stack<int>(); // Declare an empty stack of integers
Stack<string> strStack = new Stack<string>(); // Declare an empty stack of strings
We can use the Push method to add elements to the top of the stack:
Stack<int> stack = new Stack<int>();
stack.Push(1); // Add the integer 1 to the top of the stack
stack.Push(2); // Add the integer 2 to the top of the stack
We can use the Pop method to remove and return the top element from the stack:
Stack<int> stack = new Stack<int>();
stack.Push(1);
stack.Push(2);
int x = stack.Pop(); // Remove and return the top element (2) from the stack and store it in x
We can use the Peek method to return the top element from the stack without removing it:
Stack<int> stack = new Stack<int>();
stack.Push(1);
stack.Push(2);
int x = stack.Peek(); // Return the top element (2) from the stack and store it in
Queues

Queues are a data structure that follows the First In First Out (FIFO) principle, meaning that the first element added to the queue will be the first one to be removed. In C#, queues are implemented using the Queue<T> class, where T is the type of elements that the queue will store. Queues can be declared and initialized as follows:
Queue<int> queue = new Queue<int>(); // Declare an empty queue of integers
Queue<string> strQueue = new Queue<string>(); // Declare an empty queue of strings
We can use the Enqueue method to add elements to the end of the queue:
Queue<int> queue = new Queue<int>();
queue.Enqueue(1); // Add the integer 1 to the end of the queue
queue.Enqueue(2); // Add the integer 2 to the end of the queue
We can use the Dequeue method to remove and return the first element from the queue:
Queue<int> queue = new Queue<int>();
queue.Enqueue(1);
queue.Enqueue(2);
int x = queue.Dequeue(); // Remove and return the first element (1) from the queue and store it in x
We can use the Peek method to return the first element from the queue without removing it:
Queue<int> queue = new Queue<int>();
queue.Enqueue(1);
queue.Enqueue(2);
int x = queue.Peek(); // Return the first element
Sets
Sets are a data structure that stores a collection of unique elements, meaning that no element can appear more than once in a set. In C#, sets are implemented using the HashSet<T> class, where T is the type of elements that the set will store. Sets can be declared and initialized as follows:
HashSet<int> set = new HashSet<int>(); // Declare an empty set of integers
HashSet<string> strSet = new HashSet<string>(); // Declare an empty set of strings
We can use the Add method to add elements to a set:
HashSet<int> set = new HashSet<int>();
set.Add(1); // Add the integer 1 to the set
set.Add(2); // Add the integer 2 to the set
If we try to add an element that already exists in the set, it will not be added again:
HashSet<int> set = new HashSet<int>();
set.Add(1);
set.Add(2);
set.Add(2); // This will not be added to the set because 2 already exists in the set
We can use the Contains method to check if an element exists in a set:
HashSet<int> set = new HashSet<int>();
set.Add(1);
set.Add(2);
bool x = set.Contains(2); // Check if the integer 2 exists in the set and store the result in x
Dictionaries

Dictionaries are a data structure that stores a collection of key-value pairs, where each key is unique and is used to access its associated value. In C#, dictionaries are implemented using the Dictionary<TKey, TValue> class, where TKey is the type of the keys and TValue is the type of the values. Dictionaries can be declared and initialized as follows:
Dictionary<string, int> dict = new Dictionary<string, int>(); // Declare an empty dictionary with string keys and integer values
Dictionary<int, string> strDict = new Dictionary<int, string>(); // Declare an empty dictionary with integer keys and string values
We can use the index operator ([]) to add and access elements in a dictionary:
Dictionary<string, int> dict = new Dictionary<string, int>();
dict["apple"] = 1; // Add the key-value pair ("apple", 1) to the dictionary
dict["banana"] = 2; // Add the key-value pair ("banana", 2) to the dictionary
int x = dict["apple"]; // Get the value associated with the key "apple" and store it in x
We can use the ContainsKey method to check if a key exists in a dictionary:
Dictionary<string, int> dict = new Dictionary<string, int>();
dict["apple"] = 1;
dict["banana"] = 2;
bool x = dict.ContainsKey("apple"); // Check if the key "apple" exists in the dictionary and store the result in x
Linked Lists

Linked lists are a data structure that stores a collection of elements in a linear fashion, with each element pointing to the next one. Linked lists are useful when we need to insert or remove elements from the middle of the list, as they do not require the movement of other elements like arrays do. In C#, linked lists are implemented using the LinkedList<T> class, where T is the type of elements that the linked list will store. Linked lists can be declared and initialized as follows:
LinkedList<int> linkedList = new LinkedList<int>(); // Declare an empty linked list of integers
LinkedList<string> strLinkedList = new LinkedList<string>(); // Declare an empty linked list of strings
We can use the AddFirst and AddLast methods to add elements to the beginning and end of the linked list, respectively:
LinkedList<int> linkedList = new LinkedList<int>();
linkedList.AddFirst(1); // Add the integer 1 to the beginning of the linked list
linkedList.AddLast(2); // Add the integer 2 to the end of the linked list
We can use the First and Last properties to access the first and last elements of the linked list:
LinkedList<int> linkedList = new LinkedList<int>();
linkedList.AddFirst(1);
linkedList.AddLast(2);
int x = linkedList.First.Value; // Get the value of the first element of the linked list and store it in x
int y = linkedList.Last.Value; // Get the value of the last element of the linked list and store it in y
We can use the AddBefore and AddAfter methods to add elements before or after a specific element in the linked list:
LinkedList<int> linkedList = new LinkedList<int>();
linkedList.AddFirst(1);
linkedList.AddLast(2);
LinkedListNode<int> node = linkedList.First; // Get a reference to the first element of the linked list
linkedList.AddAfter(node, 3); // Add the integer 3 after the first element
linkedList.AddBefore(node, 4); // Add the integer 4 before the first element
We can use the Remove method to remove a specific element from the linked list:
LinkedList<int> linkedList = new LinkedList<int>();
linkedList.AddFirst(1);
linkedList.AddLast(2);
LinkedListNode<int> node = linkedList.First; // Get a reference to the first element of the linked list
linkedList.Remove(node); // Remove the first element from the linked list
Graphs
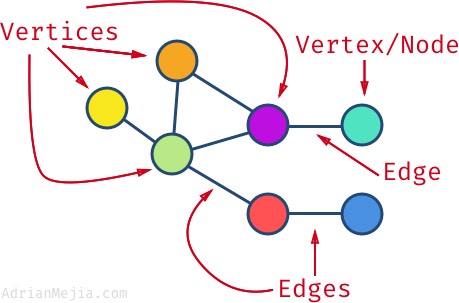
Graphs are a data structure that consists of a set of vertices (also called nodes) and a set of edges that connect the vertices. Graphs are useful for representing relationships between objects, and are commonly used for tasks such as network analysis and route finding. In C#, graphs can be implemented using a custom class or by using the Dictionary<TKey, TValue> class.
Here is an example of a custom class for implementing a graph in C#:
public class Graph
{
// A dictionary to store the vertices of the graph, where the key is the vertex name and the value is the vertex object
public Dictionary<string, Vertex> Vertices { get; set; }
// A constructor to initialize the graph
public Graph()
{
Vertices = new Dictionary<string, Vertex>();
}
// A method to add a vertex to the graph
public void AddVertex(string name, object data = null)
{
Vertices[name] = new Vertex(name, data);
}
// A method to add an edge between two vertices
public void AddEdge(string source, string destination, int weight = 1)
{
Vertices[source].AddNeighbor(Vertices[destination], weight);
}
}
// A class to represent a vertex in the graph
public class Vertex
{
// The name of the vertex
public string Name { get; set; }
// The data associated with the vertex
public object Data { get; set; }
// A dictionary to store the neighbors of the vertex, where the key is the neighbor vertex and the value is the weight of the edge
public Dictionary<Vertex, int> Neighbors { get; set; }
// A constructor to initialize the vertex
public Vertex(string name, object data = null)
{
Name = name;
Data = data;
Neighbors = new Dictionary<Vertex, int>();
}
// A method to add a neighbor to the vertex
public void AddNeighbor(Vertex neighbor, int weight = 1)
{
Neighbors[neighbor] = weight;
}
}
We can use the Graph class as follows:
Graph graph = new Graph();
// Add some vertices to the graph
graph.AddVertex("A");
graph.AddVertex("B");
graph.AddVertex("C");
graph.AddVertex("D");
// Add some edges to the graph
graph.AddEdge("A", "B");
graph.AddEdge("B", "C", 2);
graph.AddEdge("C", "D", 3);
graph.AddEdge("A", "D", 4);
This will create a graph with four vertices (A, B, C, and D) and four edges connecting them. The edge between B and C has a weight of 2, the edge between C and D has a weight of 3, and the edge between A and D has a weight of 4.
When To Use Each Of Them?
Use an array when you need to store a fixed-size collection of elements and you don't need to insert or remove elements from the middle of the collection. Arrays are also useful when you need to store elements of the same type and you don't need to search for elements frequently.
Use a list when you need to store a variable-size collection of elements and you need to insert or remove elements from the middle of the collection. Lists are also useful when you need to store elements of the same type and you need to search for elements frequently.
Use a stack when you need to store a collection of elements and you only need to access the last element added. Stacks are useful when you need to implement undo/redo functionality or when you need to evaluate expressions.
Use a queue when you need to store a collection of elements and you only need to access the first element added. Queues are useful when you need to process elements in the order they were added or when you need to implement a first-come, first-served policy.
Use a set when you need to store a collection of unique elements and you don't care about the order of the elements. Sets are useful when you need to remove duplicate elements from a collection or when you need to check if an element exists in a collection.
Use a dictionary when you need to store a collection of key-value pairs and you need to access the values by their keys. Dictionaries are useful when you need to store elements that have a unique identifier (the key) and you need to retrieve them quickly.
Use a linked list when you need to store a variable-size collection of elements and you need to insert or remove elements from the middle of the collection. Linked lists are useful when you need to preserve the order of the elements and you don't need to search for elements frequently.
Use a tree when you need to store a hierarchical collection of elements and you need to access the elements in a specific order (e.g., in-order, pre-order, post-order). Trees are useful when you need to implement a search algorithm or when you need to sort a collection of elements.
Use a graph when you need to store a collection of elements and their relationships with each other. Graphs are useful when you need to represent a network of objects or when you need to find the shortest path between two elements.
Summarized Difference
Here is a table summarizing the main differences between the data structures covered in this article:
| Data Structure | Fixed Size | Element Order | Insert/Remove | Search |
| Array | Yes | Preserved | Difficult | Fast |
| List | No | Preserved | Easy | Fast |
| Stack | No | Reversed | Easy | Fast |
| Queue | No | Preserved | Easy | Fast |
| Set | No | Unordered | Easy | Fast |
| Dictionary | No | Unordered | Easy | Fast |
| Linked List | No | Preserved | Easy | Slow |
| Tree | No | Ordered | Difficult | Slow |
| Graph | No | Unordered | Easy | Varies |
"Fixed Size" refers to whether the data structure has a fixed size that cannot be changed after it is created.
"Element Order" refers to whether the data structure preserves the order in which the elements were added.
"Insert/Remove" refers to the ease of inserting and removing elements from the data structure.
"Search" refers to the speed at which elements can be searched in the data structure.
